Baidu is reportedly planning to launch a subsidiary AI chip firm, which could boost China‘s efforts to develop a domestic semiconductor industry.

CNBC reports that the search giant is in talks with venture capital firms GGV and IDG Capital about investing in the venture.

The company would sell chips to customers in various industries, including automakers, and could also support Baidu’s work on electric and autonomous vehicles.

A source told CNBC that Baidu would likely be the majority shareholder of the subsidiary.

The news comes as China pushes to strengthen its homegrown chip sector.

The country’s reliance on foreign gear has been exposed by the trade war with the US, which last year imposed a series of restrictions on sales of chips and components to China.

China responded by setting a goal of producing 70% of the semiconductors it uses by 2025.

The target is certainly ambitious: only 16% of the semiconductors it used in 2019 were made indigenously.

The country is relying on government investment and domestic corporations to become more self-sufficient.

CNBC notes that tech giant Tencent recently invested in an AI chip startup, while Alibaba and Huawei both unveiled AI semiconductors in 2019.

Baidu’s subsidiary would further support China’s drive for self-sufficiency, but the country is still a long way from building a world-leading chip industry.

Sure, DeepMind’s AI is impressive, but can it guide human intuition?

This article is part of our reviews of AI research papers , a series of posts that explore the latest findings in artificial intelligence.

Deep learning can help discover mathematical relations that evade human scientists, a recent paper by researchers at DeepMind shows. Like many things coming from the Alphabet-owned artificial intelligence lab, the paper, which is titled “ Advancing mathematics by guiding human intuition with AI ,” has received much attention from science and tech media.

Some mathematicians and computer scientists have lauded DeepMind’s efforts and the findings in the paper as breakthroughs. Others are more skeptical and believe that the use of deep learning in mathematics might have been overstated in the paper and its coverage in popular press.

The results are nonetheless fascinating and can expand the toolbox of scientists in discovering and proving mathematical theorems.

A framework for mathematical discovery with machine learning

In their paper, the scientists at DeepMind suggest that AI can be used to “assist in the discovery of theorems and conjectures at the forefront of mathematical research.” They propose a “framework for augmenting the standard mathematician’s toolkit with powerful pattern recognition and interpretation methods from machine learning.”

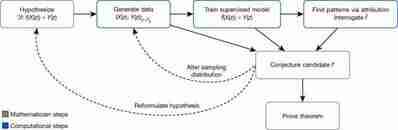
Mathematicians start by making a hypothesis about the relation between two mathematical objects. To verify the hypothesis, they use computer programs to generate data for both types of objects. Next, a supervised machine learning model algorithm crunches the numbers and tries to tune its parameters that map one type of object to the other.

“The key contributions of machine learning in this regression process are the broad set of possible nonlinear functions that can be learned given a sufficient amount of data,” the researchers write.

If the trained model performs better than random guessing, then it might indicate that there is indeed a discoverable relation between the two mathematical objects. Using various machine learning techniques, the researchers can find the data points that are more relevant to the problem, reform their hypothesis, generate new data, and train new models. By repeating these steps, they can narrow down the set of plausible conjectures and speed their way toward a final solution.

DeepMind’s scientists describe the framework as a “test bed for intuition” that can quickly verify “whether an intuition about the relationship between two quantities may be worth pursuing” and provide guidance as to how they may be related.

Using this framework, the DeepMind researchers used deep learning to reach “two fundamental new discoveries, one in topology and another in representation theory.”

An interesting aspect of the work was that it did not require the huge amount of compute power that has become a mainstay of DeepMind’s research. According to the paper, the deep learning models used in both discoveries can be trained “within several hours on a machine with a single graphics processing unit.”

Knots and representations

Knots are closed loops in dimensional space that can be defined in various ways. They become more complex as the number of their crossings grows. The researchers wanted to see whether they could use machine learning to discover a mapping between algebraic invariants and hyperbolic invariants, two fundamentally different ways of defining knots.

“Our hypothesis was that there exists an undiscovered relationship between the hyperbolic and algebraic invariants of a knot,” the researchers write.

Using the SnapPy software package, the researchers generated the “signature,” an algebraic invariant, and 12 promising hyperbolic invariants for 1.7 million knots with up to 16 crossings.

Next, they created a fully connected, feed-forward neural network with three hidden layers, each having 300 units. They trained the deep learning model to map the values of the hyperbolic invariants to the signature. Their initial model was able to predict the signature with 78 percent accuracy. Further analysis brought them to a smaller set of parameters in the hyperbolic invariants that were predictive of the signature. The researchers refined their conjecture, generated new data, retrained their models, and reached a final theorem.

The researchers describe the theorem as “one of the first results that connect the algebraic and geometric invariants of knots and has various interesting applications.”

“We expect that this newly discovered relationship between natural slope and signature will have many other applications in low-dimensional topology. It is surprising that a simple yet profound connection such as this has been overlooked in an area that has been extensively studied,” the researchers write.

The second result in the paper is also a mapping of two different views of symmetries, a problem that is much more complicated than knots.

In this case, they used a type of graph neural network (GNN) to find relations between Bruhat interval graph and the Kazhdan-Lusztig (KL) polynomial. One of the benefits of GNNs is that they can compute and learn graphs that are very large and hard to manage for the unaided mind. The deep learning model takes the interval graph as input and tries to predict the corresponding KL polynomial.

Again, by generating data, training DL models, and readjusting the process, the scientists were able to formulate a provable conjecture.

Reactions to DeepMind’s math AI

Speaking about DeepMind’s discovery in knot theory, Mark Brittenham, a knot theorist at the University of Nebraska–Lincoln told Nature , “The fact that the authors have proven that these invariants are related, and in a remarkably direct way, shows us that there is something very fundamental that we in the field have yet to fully understand.” Brittenham added that, in comparison to other efforts to apply machine learning to knots, DeepMind’s technique is novel in its ability to discover surprising connections.

Adam Zsolt Wagner, a mathematician at Tel Aviv University, Israel, who also spoke to Nature, said that the methods presented by DeepMind could prove valuable for certain kinds of problems.

Wagner, who has experience in applying machine learning to mathematics, said, “Without this tool, the mathematician might waste weeks or months trying to prove a formula or theorem that would ultimately turn out to be false.” But he also added that it is unclear how broad its impact will be.

Reasons to be skeptical

Following the publication of DeepMind’s work in Nature, Ernest Davis, Computer Science Professor at New York University, published a paper of his own , which raises some important questions about DeepMind’s framing of the results and the limits of applying deep learning to mathematics in general.

On the first result presented in DeepMind’s paper, Davis observes that knot theory is not the kind of problem where deep learning typically outshines other machine learning or statistical methods.

“DL’s strength is in cases like vision or text where each instance (image or text) has a large number of low-level input features, it is hard to reliably identify high-level features, and the function relating the input features to the answer is, as far as anyone can tell, immensely complex, with no small subset of the input features being at all determinative,” Davis writes.

The knot problem had only twelve input features, of which only three turned out to be relevant. And the mathematical relation between the input features and target variable was simple.

“It is hard to see why a neural network with 200,000 parameters would be the method of choice; simple, conventional statistical methods or a support vector machine would be more suitable,” Davis writes.

In the second project, the role of deep learning was much more relevant, Davis notes. “Unlike the knot theory project, which used a generic DL architecture, the neural network was carefully designed to fit deep mathematical knowledge about the problem. Moreover, the DL worked much better, with something like 1/40th the error rate, on pre-processed data than on the original data,” he writes.

On the one hand, the results cut against criticism pertaining that it is hard to incorporate domain knowledge into deep learning, Davis notes. “On the other hand, enthusiasts for DL have often praised DL as a ‘plug-and-play’ learning methodology that can be thrown at raw data for whatever problem comes to hand; this cuts against that praise,” he writes.

Davis also notes that the success of applying deep learning to these tasks may depend critically on the way the training data is generated and the way that the mathematical structures are encoded. This suggests that the framework might be applicable to a narrow class of mathematical problems.

“Finding the best way to generate and encode data involves a mixture of theory, experience, art, and experimentation. The burden of all this lies on the human expert,” he writes. “Deep learning can be a powerful tool, but it is not always a robust one.”

Davis warns that in the current climate of hype surrounding deep learning, “there is a perverse incentive to focus the role of the DL in this research, not just for the ML specialists from DeepMind, but even for the mathematicians.”

Davis concludes that, as used in the paper, deep learning is best viewed as “another analytic tool in the toolbox of experimental mathematics rather than as a fundamentally new approach to mathematics.”

It is worth noting that the authors of the original paper have also pointed out some of the limits of their framework, including that “it requires the ability to generate large datasets of the representations of objects and for the patterns to be detectable in examples that are calculable. Further, in some domains the functions of interest may be difficult to learn in this paradigm.”

Deep learning and intuition

One of the topics of controversy is the paper’s claim that deep learning is “guiding intuition.” Davis describes this claim as a “seriously inaccurate description of the assistance that mathematicians have gained, or can hope to gain, from this use of DL systems.”

Intuition is one of the key differentiators between human and artificial intelligence. It is the ability to make decisions that are better than random guesses and can direct you in the right direction most of the time. As the history of AI has so far shown, intuition is not captured in countless predefined rules or patterns found in vast amounts of data.

“In the mathematical setting, the word ‘intuitive’ means that a concept or a proof can be grounded in a person’s deep-seated sense of familiar domains such as numerosity, space, time, or motion, or in some other way ‘makes sense’ or ‘seems right’ in a way that does not involve explicit calculation or step-by-step reasoning,” Davis writes.

While obtaining an intuitive grasp of mathematical concepts often requires working through multiple specific examples, it is not a work of statistical correlations, Davis argues. In other words, you don’t gain intuitions by running millions of examples and observing the percent of times certain patterns recur.

This means that it was not the deep learning models that provided the scientists with an intuitive understanding of the concepts they defined, the theorems they proved, and the conjectures they put forward.

Writes Davis, “What the DL did was to give them some advice as to which features of the problem seemed to be important and which seemed unimportant. That is not to be sneezed at, but it should not be exaggerated.”

This article was originally published by Ben Dickson on TechTalks , a publication that examines trends in technology, how they affect the way we live and do business, and the problems they solve. But we also discuss the evil side of technology, the darker implications of new tech, and what we need to look out for. You can read the original article here .

Spider legs build webs without the brain’s help — and could inspire robot limbs

Arachnophobes often cite spiders’ unpredictable movement as the basis of their fear, pointing out how each spindly leg seems to lift, flex, and probe with a menacing degree of autonomy.

Perhaps unsettlingly, research conducted by my colleagues and I has revealed that each one of a spider’s legs does indeed enjoy a certain independence from the brain – especially in the complex task of web-building.

Our study has shown that spider legs have “minds of their own,” constructing webs without the oversight of the spider’s brain. This has important implications for the field of robotics, which may take inspiration from this example of decentralized intelligence to build similarly autonomous robot limbs.

To arrive at our conclusions, we observed the common garden spider Araneus diadematus , a creature familiar to us all – both suspended in our backyards, and as the heroine within the pages of the children’s book Charlotte’s Web.

Web engineers

Spiders’ webs serve many functions. They provide a safe home, but they’re also famously an invisible and highly dynamic trap set up to capture and then firmly hold any insect that strays too close.

To perform this function, webs use a strong structural scaffold of radiating spokes with what’s called a “capture spiral” built on top, which is soft and sticky and uses an extremely clever microscopic reeling mechanism to pull in a spider’s prey.

Not only does the capture spiral use electrostatic charges to trap a fly, it features a complex glue to hold it firmly, and a specific elasticity that makes the web too stretchy for the leg of a hapless insect to push against in its struggle for freedom.

The analogy of the internet as a “web” is a fine one: because at least five different silks are used in a spider’s web, the way they intersect and network with one another creates a kind of information filtering capacity – with tiny vibrations noted at all times by a spider’s listening legs.

Spider diagram

Given the incredible complexity of spiders’ webs, we must ask how such a small animal – with an obviously minute brain – can design and build this advanced structure. Modern technology has helped us begin to understand how spiders manage such a complex task.

By filming and tracking the movements of its eight legs, we have been able to track a spider’s web-building in intimate detail, revealing the construction process to be a kind of dance around a central hub, with a precise choreography of replicable rules.

These rules are surprisingly simple. Each step and thread manipulation follows a fixed action pattern, with one of the spider’s legs measuring an angle and a distance in order to place and then connect one thread to another with a quick dab of glue – always with impeccable accuracy and spacing. Many years ago, we programmed a virtual spider, named Theseus, to demonstrate how this works.

Outsourcing

The complexity of the task at hand (or rather foot) when building a web seems to have required spider brains to outsource the work to the eight legs. Put another way, spider legs build webs semi-autonomously – eight phantom limbs performing their dance within local, closed feedback loops.

We discovered this after studying spiders building webs within frames in our laboratory. In some experiments, we cut out threads of a web being built. In others, we rotated the web like a ferris wheel. This probing wasn’t done to annoy the spider: it was to help us discern the rules that govern web building.

With a set of rules established – including rules that help spiders continue to build a disrupted web – we taught them to Theseus, our virtual spider.

The new rules we taught Theseus – based on the dances of real spiders we observed in our lab – revealed that each leg actually conducts many web-building actions as an independent agent . This in turn helped us solve the mystery of how spiders build perfect webs after the loss of a leg.

When a spider’s leg becomes trapped, it’s discarded, and a shorter leg regenerates the next time the spider molts its exoskeleton. Not only is this replacement half the size of a normal leg, but it’s also a different shape, with different hairs and sensors. Yet somehow spiders with regenerated legs continue to build perfect webs.

Evolution has seen to it that spider legs can in some sense think for themselves, which means the different properties of regenerated legs does not affect the building of a web.

This relieves the brain from micromanaging eight legs executing complicated activities, freeing it to focus on survival actions such as looking out for predators. This efficient, decentralized system is remarkably relevant for modern roboticists – who are often inspired by the natural world in their artificial designs.

Spiders are not alone in decentralizing tasks from the brain – indeed, most animals do it to some extent, like the continuous beating of a human heart. But with their webs, spiders provide us with a concrete, observable, and mesmerizing means of measuring and understanding how this decentralization works.

This neat trick lies in a spider’s embedding of simple task computation within the structure of its limbs. Roboticists call this morphological computing and have only relatively recently discovered its power. The humble garden spider, it turns out, has been using it for well over 100 million years.

This article by Fritz Vollrath , Emeritus Professor, Department of Zoology, University of Oxford is republished from The Conversation under a Creative Commons license. Read the original article .